Image Processing Reference
In-Depth Information
Effects of Turbulence on a Wavefront
21
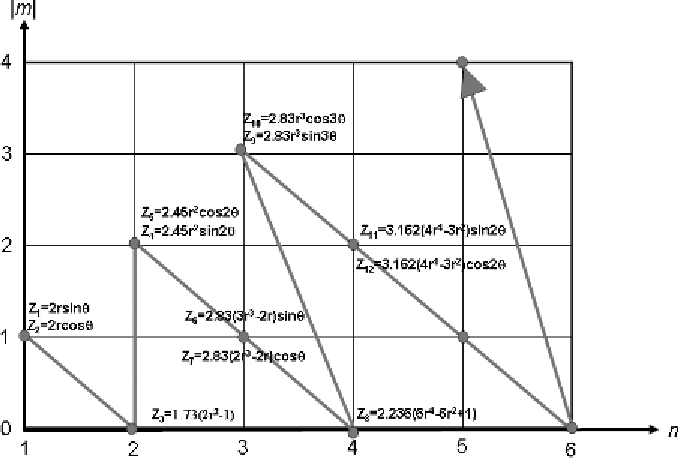
Figure 2.10
One way to enumerate the Zernike polynomials. Following the line
through the points on the graph provides the row sequence of Zernike polynomials,
beginning at the lower left of Fig. 2.8 and up through the rows in sequence.
tical system. In this case, piston is used in combination with other Zernike polyno-
mials to provide an offset so that the contributions of the higher-order polynomials
are equally weighted around a central point set by the magnitude of the piston term
(Noll 1976; Malacara 1992).
2.6 Global Tip and Tilt
Wavefronts composed of combinations of Zernike modes have detailed structures
on a scale much smaller than the full entrance aperture or pupil of a telescope.
When compared to an ideal or reference wavefront, the spatial structure can be
identified and analyzed. It is convenient to be able to remove certain modes from
the wavefront that, while they do not contribute to the small-scale structure, can be
of large amplitude.
Most common is the overall tip and tilt of the wavefront. The small-scale struc-
ture induces a local slope in the wavefront; however, it is rare that the average slope
across the wavefront is zero. Thus, for any wavefront, a global tip and tilt can be de-
termined. Using the wavefront shown in Fig. 2.9, we can extract the local tip across
the wavefront and then calculate the global tilt on the entire wavefront. This is
shown in Fig. 2.11, and demonstrates that the residual structure in the wavefront
can be enhanced when the global tilt is subtracted.