Information Technology Reference
In-Depth Information
a
i
+
(
a
i
b
i
−
x
−
a
i
b
i
−
y
−
2
b
i
−
a
i
)
T
i
(
a
i
,
a
i
),
if
(
x
,
y
)
∈[
a
i
,
b
i
]
T
(
x
,
y
)
=
min
(
x
,
y
),
otherwise,
1
.
The continuous t-norm of the fourth type are called
ordinal-sums
of the continuous
t-norms
T
i
for any x
,
yin
[
0
,
.
Remark 2.2.34
Why the names t-norm and t-conorm? The “t” comes from “triangu-
lar”, because these functions were introduced to formalize the triangular property of
probabilistic distances, i.e. distances whose values are something like the probability
that the numerical distance between two points is less than a given number. They
were introduced by Karl Menger with the name triangular-norms without considering
associativity.
The name of t-conorm refers to the duality with a t-norm, since
S
is a t-conorm
if and only if 1
∈{
pr od
}∪{
W
}
is a t-norm. In general, it should be pointed out
that, for each strong negation
N
,
S
is a t-conorm if and only if
N
−
S
(
1
−
x
,
1
−
y
)
ⓦ
S
ⓦ
(
N
×
N
)
is a
t-norm.
Theorem 2.2.35
S
is a continuous t-conorm if and only if,
1.
S
=
max
, S is in the family of max
pr od
˕
, S is in the family of prod
∗
=
2.
S
W
˕
, S is in the family of W
∗
=
3.
S
4.
There exist an index set
(
finite or countable infinite
)
, a family of pairwise dis-
joint open intervals of
[
0
,
1
]
,
{
(
a
1
,
b
1
)
;
i
∈
I
}
, and a family of t-conorms
pr od
∗
}∪{
W
∗
}
(
S
i
∈{
i
∈
I
)
, such that
a
i
+
(
a
i
b
i
−
x
−
a
i
b
i
−
y
−
2
b
i
−
a
i
)
S
i
(
a
i
,
a
i
),
if
(
x
,
y
)
∈[
a
i
,
b
i
]
S
(
x
,
y
)
=
max
(
x
,
y
),
otherwise,
for any x
,
yin
[
0
,
1
]
.
Remark 2.2.36
Notice that with both ordinal-sums of t-norms and of t-conorms,
provided it is
[
0
,
1
]=[
0
,
b
1
]∪[
b
1
,
b
2
]···∪[
b
n
−
1
,
b
n
]∪[
b
n
,
1
]
, a finite partition
of the unit interval
[
0
,
1
]
, like, for example













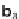






Search WWH ::

Custom Search