Information Technology Reference
In-Depth Information
2.2.7 Continuous T-Norms and T-Conorms
As it was said, the only t-norm that is idempotent for all
a
in
[
0
,
1
]
,is
T
=
min, and
the t-norms in
only have the idempotents 0 and 1. As it was also said,
there are t-norms with several (but not all) idempotent elements. For example, the
function
{
pr od
}∪{
W
}
3
+
1
1
2
2
3
W
(
3
x
−
1
,
3
y
−
1
),
if
(
x
,
y
)
∈[
3
,
3
]
T
(
x
,
y
)
=
min
(
x
,
y
),
otherwise
,
1
0.8
min
0.6
2/3
W
0.4
1/3
0.2
0
1
2/3
1/3
0.5
1
0.8
0.6
0.4
0
0.2
0
that as it is easy to prove is a t-norm, verifies
1
2
•
T
(
x
,
x
)
=
min
(
x
,
x
)
=
x
,
if
x
/
∈[
3
,
3
]
1
1
1
1
1
1
1
3
•
T
(
3
,
3
)
=
3
+
3
W
(
0
,
0
)
=
3
+
3
.
0
=
2
2
1
1
1
1
2
3
•
T
(
3
,
3
)
=
3
+
3
W
(
1
,
1
)
=
3
+
3
=
1
1
1
1
2
2
1
1
1
1
1
1
1
1
2
•
T
(
2
,
2
)
=
3
+
3
W
(
3
−
1
,
3
−
1
)
=
3
+
3
W
(
2
,
2
)
=
3
+
3
.
0
=
3
=
•
etc.
1
2
,aswell
3
2
3
that is, all elements in
[
0
,
1
]−[
3
,
3
]
and
are idempotent for
T
, and the
1
2
elements in
are not idempotent.
Look that an analogous result is obtained when changing
W
by prod in the above
expression of
T
. Without proof it follows the theorem that completely characterizes
all continuous t-norms.
(
3
,
3
)
Theorem 2.2.33
T is a continuous t-norm if and only if,
=
1.
T
min
, T is in the family of min
2.
T
=
pr od
˕
, T is in the family of prod
3.
T
=
W
˕
, T is in the family of W
4.
There exist an index set
(
finite or countable infinite
)
, a family of pairwise disjoint
open intervals in
[
0
,
1
]
,
{
(
a
1
,
b
1
)
;
i
∈
I
}
, and a family of t-norms T
i
∈{
pr od
}∪
{
W
}
(
i
∈
I
)
, such that

























































































































































































































































































































































































































































































































































































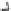






















































































































































































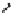
























































































































































Search WWH ::

Custom Search