Information Technology Reference
In-Depth Information
•
The height of
μ
∈
F
(
X
)
is
H
(μ)
=
Sup
x
X
μ(
x
)
=
sup
μ
. In the last example, it is
∈
H
(μ)
=
1. In the finite example
μ
=
0
.
7
/
x
1
+
0
.
9
/
x
2
+
0
.
7
/
x
3
,
in
X
={
x
1
,
x
2
,
x
3
,
x
4
}
,itis
H
(μ)
=
0
.
9. In a case like
(μ)
=
∈ R
μ(
)
=
it is
H
1, although there is not any
x
such that
x
1. If there is
∈
μ(
)
=
μ
some
x
X
such that
x
1, it is said that
is a
normalized
fuzzy set.
•
In the case
X
is finite,
X
={
x
1
,...,
x
n
}
, the number
n
|
μ
|=
1
μ(
x
i
)
i
=
is the
crisp-cardinality
, or sigma-count, of
μ
, a name coming from the fact that if
X
has
p
elements it is
i
=
1
μ(
A
ↆ
x
i
)
=
p
. Obviously,
μ
∅
=
μ
0
,gives
|
μ
0
|=
0,
μ
X
=
μ
1
,gives
|
μ
1
|=
n
, and,
μ
˃
implies
|
μ
| |
˃
|
.
Remark 2.2.1
The pointwise definition of fuzzy sets inclusion implies that, for exam-
ple, the fuzzy sets
μ
=
0
.
7
/
x
1
+
0
.
8
/
x
2
+
1
/
x
3
+
0
.
7
/
x
4
˃
=
0
.
70001
/
x
1
+
0
.
7
/
x
2
+
1
/
x
3
+
0
.
6
/
x
4
in
X
, do not verify
μ
˃
although it is
˃(
x
2
)<μ(
x
2
), ˃(
x
3
)
=
μ(
x
3
), ˃(
x
4
)<
μ(
00001. Pointwise 'inclusion' is
strongly affected by very small variations of the membership values. Actually, it is
not a flexible, or fuzzy, concept, but a crisp one.
Because of this, it could be preferable to take the inclusion of fuzzy sets as an
gradable concept
x
4
)
,but
˃(
x
1
)>μ(
x
1
)
, with
˃(
x
1
)
−
μ(
x
1
)
=
0
.
r
(
∈[
,
]
)
r
0
1
, and a used definition of which is










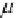








Search WWH ::

Custom Search