Information Technology Reference
In-Depth Information
a
+
•
ₒ
=
(
,
)
=
(
(
),
)
[
,
]
S
-implications:
a
b
b
and
J
a
b
S
N
a
b
for all
a
,
b
in
0
1
,
with some strong negation function
N
and some continuous t-conorm
S
.
a
+
•
R
-implications:
a
ₒ
b
=
b
and
J
(
a
,
b
)
=
Sup
{
z
∈[
0
,
1
];
T
(
z
,
a
)
b
}=
J
T
(
a
,
b
))
for all
a
,
b
in
[
0
,
1
]
and some continuous t-norm
T
.
a
+
•
Q
-implications:
a
ₒ
b
=
a
·
b
and
J
belongs to the family
J
(
a
,
b
)
=
S
(
N
(
a
),
T
(
a
,
b
)
.
•
ML
-implications:
a
ₒ
b
=
a
·
b
and
J
is in the family of functions
J
(
a
,
b
)
=
T
(
a
,
b
)
.
In fuzzy control mostly ML-implications are considered. Since
T
is a continu-
ous t-norm, it is
T
˕
=
˕
−
1
=
Min
,or
T
=
Prod
ⓦ
Prod
ⓦ
(˕
×
˕)
,or
˕
=
˕
−
1
T
=
W
ⓦ
W
ⓦ
(˕
×
˕)
, with
˕
an order-automorphism of the unit
interval (
.Of
course,
T
can be also an ordinal-sum, but these t-norms have never been considered
in fuzzy logic. Hence, a
ML
-implication belongs to the types:
J
M
(
[
0
,
1
]
,
),
Prod
(
x
,
y
)
=
x
·
y
and
W
(
x
,
y
)
=
Max
(
0
,
x
+
y
−
1
)
a
,
b
)
=
Min
(
a
,
b
)
,
J
L
(
a
,
b
)
=
Prod
˕
(
a
,
b
)
and
J
W
(
a
,
b
)
=
W
˕
(
a
,
b
)
. Only in the third type we can
have
J
(
a
,
b
)
=
0 with
a
=
0 and
b
=
0, since it is
W
˕
(
a
,
b
)
=
0 whenever
˕(
a
)
+
˕(
b
)
1, and as in fuzzy control it is desirable not only that
a
=
0 implies
J
(
a
,
b
)
=
0 but also that
a
=
0 and
b
=
0imply
J
(
a
,
b
)
=
0, the third type is rarely
used and only
J
M
(
b
(Larsen implication) are almost always considered. Notice that for all
S
, and
Q
implication functions it is:
J
a
,
b
)
=
Min
(
a
,
b
)
(Mamdani implication) and
J
L
(
a
,
b
)
=
a
·
(
0
,
b
)
=
1.
Second Step: Modus Ponens
Rules are used in our problem to infer
μ
Q
∗
, and this inference requires that when the
states of the input variables
x
1
,...,
x
n
are exactly those appearing in the antecedent
part of one of the
m
rules, say rule number
i
, then
μ
Q
∗
should be the consequent
μ
Q
i
of this rule. That is, each rule should satisfy the meta-rule of Modus Ponens:
This meta-rule is satisfied when there is a continuous t-norm
T
1
such that
T
1
(μ
P
∗
(
x
),
R
(μ
P
, μ
Q
)(
x
,
y
))
μ
Q
∗
(
y
),
for all
x
∈
X
,
y
∈
Y
. When
R
(μ
P
, μ
Q
)(
x
,
y
)
=
J
(μ
P
(
x
), μ
Q
(
y
))
,thelast
inequation is
T
1
(μ
P
∗
(
x
),
J
(μ
P
(
x
), μ
Q
(
y
))
μ
Q
∗
(
y
),
for all
x
Y
.
Hence, for each type of implication function
J
we need to know which
T
1
allows
the verification of the Modus Ponens inequality:
∈
X
,
y
∈
T
1
(
a
,
J
(
a
,
b
))
b
,
for all
a
,
b
∈[
0
,
1
]
.





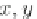




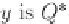
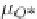


Search WWH ::

Custom Search