Game Development Reference
In-Depth Information
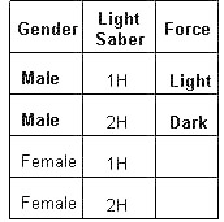
Figure 10.3
Adding Force choices for the Male rows.
Figure 10.4
Adding the first Force choice for the Female character tests.
Finally, fill in the Light value in the second Female row to get the table in Figure 10.5 that
satisfies the pairwise criteria for all parameters. In this case, it ends up being the same size
as the two-parameter table. Including the Force parameter in these tests is free in terms of
the resulting number of test cases. In many cases, pairwise combinatorial tables let you add
complexity and coverage without increasing the number of tests you will need to run. This
will not always be true; sometimes you will need a few more tests as you continue to add
parameters to the table. However, the growth of the pairwise table will be much slower
than full combinatorial tables for the same set of parameters and their values.
In this simple example, the pairwise technique has cut the number of required tests in
half as compared to creating every mathematically possible combination of all of the
parameters of interest. This technique and its benefits are not limited to tables with
two-value parameters. Parameters with three or more choices can be efficiently com-
bined with other parameters of any dimension. When it makes sense, incorporate
more parameters to make your tables more efficient.