Information Technology Reference
In-Depth Information
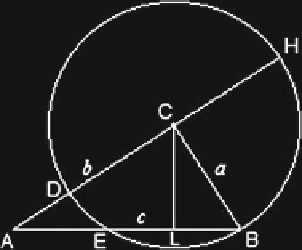
Fig. 18.3
Proof #59 in [
1
]
#59 and #60 in [
1
] use the “Intersecting Chords Theorem” in two different ways,
and proof #64 uses Socrates' Theorem. Let us follow proof #59 as given in [
1
]
(see Fig.
18.3
):
Let
BC
=
a
be the shorter of the two legs of the right angle of the triangle, and
c
. With
C
as center
and radius
a
describe a circle. Let
D
be the intersection of
AC
with the circle,
H
the other one obtained by extending
AC
beyond
C
, and
E
the intersection of
AB
with the circle. Draw
CL
perpendicular to
AB
.
L
is the midpoint of
BE
.
By the Intersecting Chords Theorem, we have:
AC
=
b
be the longer one. Also, let the hypotenuse
AB
=
(
AH
)
·
(
AD
)
=
(
AB
)
·
(
AE
)
.In
other words:
. Now, the right triangles
ABC
and
BCL
share an angle at
B
and, therefore, are similar. Hence,
BL
(
b
+
a
)(
b
−
a
)
=
c
(
c
−
2
BL
)
/
BC
=
BC
/
AB
,
a
2
c
. Combining all together we have:
b
2
a
2
2
a
2
so that
BL
=
/
−
=
c
(
c
−
/
c
)
.
Hence,
a
2
c
2
, i.e., the Pythagorean relation obtains.
Proof #60 proceeds in a similar fashion, based on the idea that the circle has radius
b
, the length of the longer leg. However, both proofs #59 and #60 fail if triangle
ABC
is not only right but also isosceles, with
CA
b
2
+
=
a
). In that
case, the problem reduces directly to the above-mentioned “Socrates' Theorem”,
referring to the simple statement that the area of a right isosceles triangle with
hypotenuse
k
equals
k
2
=
CB
(or:
b
=
4. Socrates' proof is independent of the Pythagorean
Theorem, so there is no circular reasoning in it.
At this point, however, it could be that agent
A
1
misses the fact that the previ-
ous proof fails in the above special case, i.e., if triangle
ABC
is not only right
but also isosceles. Once
A
1
posts the proof on the system, codelets (interpreters)
that verify its correctness will hopefully spot the problem and spawn new ones,
with the task of solving it. The solution could be given immediately by a codelet
(prover) that observes that the problematic special case is merely an instantiation
of Socrates' Theorem.
Let us now consider Proof #64 in [
1
], explicated by Fig.
18.4
. Here, the sides of
the given triangle
ABC
have been extended in the manner suggested in Fig.
18.4
,
forming the square
CDFH
. In addition, given the fixed lengths
a
and
b
on the
sides of the square, lines
BE
,
EG
, and
GB
have been drawn. The proof proceeds
as follows:
The equal triangles
ABC
and
ADE
have areas equal to
ab
/
/
2. The isosceles
right triangle
ABE
has area
c
2
/
2 (which is given by Socrates' Theorem, not by

Search WWH ::

Custom Search