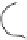Database Reference
In-Depth Information
A
A
q
o
q
p
p
B
B
a
b
Objects
p
and
q
are density-connected,
i.e., they can build a density-based cluster,
in subspaces
Objects
p
and
q
are not density-
connected in subspace
B
. Therefore they
cannot be density-connected in subspace
A
,
B
{
}
{
A, B
,
}
{
A
,and
B
.
}
{
}
{
}
either.
Fig. 16.4
Transfer of anti-monotonicity to subspace clusters
even completely irrelevant for certain clusters. If we measure similarity over the full
space, i.e., over all attributes, detecting such 'subspace' clusters becomes increas-
ingly difficult for higher numbers of irrelevant dimensions. To the end of identifying
the relevant attributes, and measuring similarity only over these, the fundamental
algorithmic idea of Apriori has been transferred to clustering in Euclidean spaces,
giving rise to the task of 'subspace clustering', which has been defined as 'finding
all clusters in all subspaces' [
7
].
Over time, this transfer has been done in different ways. The most important
variants are to identify subspace clusters that in turn qualify some subspace as 'fre-
quent pattern', or to identify interesting subspaces without direct clustering, but as
a prerequisite for subsequent clustering in these subspaces or as an integral part of
some clustering procedure.
Subspace Clusters as Patterns
Let us consider the case of clusters in different
subspaces with an example for density-based clusters [
51
], as visualized in Fig.
16.4
.
In the first scenario, depicted in Fig.
16.4
a, we see that objects
p
and
q
are density-
connected with respect to some parameters in subspaces
. Here,
the parameters capturing density are a distance threshold defining the radius of the
neighborhood ball and a minimum number of points required to fall within this
neighborhood ball in order to qualify as dense. That is, within these subspaces, we
can reach both
p
and
q
starting at
o
by 'hopping' from one object with at least
n
neighbors within
ε
distance to another. This means that with these parameters,
p
and
q
belong to the same density-based cluster in each of these subspaces.
In the second scenario, depicted in Fig.
16.4
b,
p
and
q
are again density-connected
in subspace
{
A
,
B
}
,
{
A
}
, and
{
B
}
. As a result from monotonicity, they
therefore are also not density-connected in subspace
{
A
}
, but not in subspace
{
B
}
{
A
,
B
}
.